Формулы скорость: Формула средней скорости

Скорость равномерного движения тела – формула, определение направления

Важнейшим параметром движения в кинематике является скорость. Рассмотрим особенности этой характеристики для случая равномерного движения тела.

Равномерное движение тела

Если тело движется, то путь, пройденный им постоянно увеличивается. Однако, если мы будем отмечать путь, пройденный движущимся телом за каждую секунду или каждый час (или любой другой одинаковый промежуток времени), то этот путь не обязательно будет увеличиваться. Он может и уменьшаться, и оставаться без изменения, и даже может быть нулевым (ясно, что в этом случае тело покоится на месте).

Движение, при котором за равные промежутки времени тело проходит равный путь, называется равномерным.

Рис. 1. Примеры равномерного движения.

Хотя, в природе равномерные движения достаточно редки, в жизни человека таких движений гораздо больше. Эталон равномерного движения – стрелки часов, которые каждый час проходят один и тот же путь по циферблату.

Скорость, как главная характеристика движения

На примере стрелок часов – часовой, минутной и секундной – можно видеть разницу в движении. Хотя все эти три стрелки проходят за равные промежутки времени равные пути, а значит, все три движутся равномерно, двигаются они совершенно по-разному.

Для характеристики этой разницы введено понятие скорости.

Скорость равномерного движения тела равна пути, проходимому телом за единицу времени.

Рис. 2. Скорость равномерного движения.

То есть, для нахождения скорости надо найти отношение пройденного пути ко времени, за который этот путь был пройден. Поскольку при равномерном движении тело за любой равный промежуток времени проходит одно и то же время, то это отношение будет всегда одинаковым. Формула скорости равномерного движения:

$$v={s over t},$$

где:

• $v$ – скорость;
• $s$ – путь;
• $t$ – время;

Таким образом, физический смысл скорости – это путь, проходимый телом в единицу времени. 8$ м/с.

Скорость – векторная величина

Полученное значение говорит о величине скорости. Однако, эта характеристика не единственная.

Представим себе, что нам надо через 10 часов прибыть на северный полюс, до которого 10 тысяч километров, на самолете, движущемся со скоростью тысяча километров в час. Если самолет летит точно на север, он прибудет вовремя. А что будет, если самолет полетит на восток ? Мы не достигнем цели не только через 10 часов, но и вообще никогда.

Из этого примера можно видеть важнейшую особенность скорости – она имеет направление. Величины, не имеющие направления, называются скалярными. Величины, имеющие направление, называются векторными.

Рис. 3. Скалярные и векторные величины.

Скорость – одна из векторных величин. Для полного определения скорости необходимо указывать не только ее величину, но и направление.

Что мы узнали?

Скорость равномерного движения равна отношению пройденного пути ко времени, за который этот путь был пройден.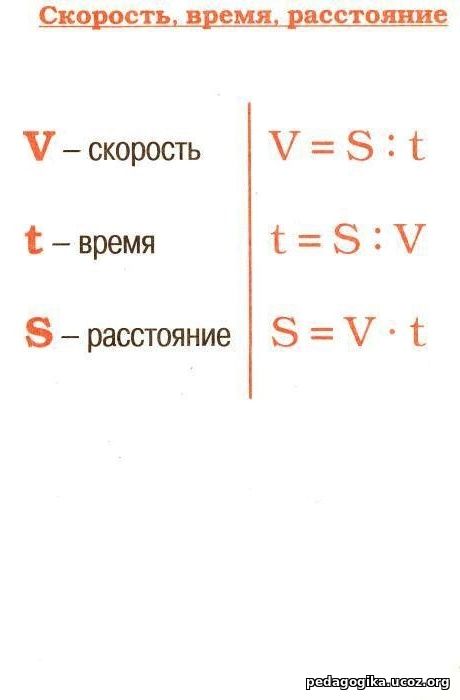 Скорость измеряется в метрах в секунду и является векторной величиной.

Предыдущая

ФизикаСвободное падение тел – формулы, определение, примеры

Следующая

ФизикаПеремещение при равноускоренном движении – формула, уравнение

Формула работы через скорость

Скорость физического тела при воздействии на него силы меняется по модулю, т.е. увеличивается или уменьшается.

Определение 1

Работу можно рассматривать как изменение кинетической энергии движущегося тела в результате действия вызвавшей это изменение силы.

В простейшем случае, когда направления движения тела и приложенной к ней силы совпадают, работа прямопропорциональна интенсивности силы и расстоянию, пройденному телом под воздействием этой силы:

$A = F \cdot s = m \cdot v \cdot s$,

где:

• $F$ — сила,
• $s$ — расстояние,
• $m$ — масса,
• $v$ — скорость.

В Международной системе СИ работа измеряется в джоулях. Один джоуль равен работе по перемещению тела силой в 1 ньютон на расстояние в 1 метр.

2}$

На практике направления векторов движения тела и совершающей работу силы могут не совпадать. В таких случаях элементарную (выполненную на бесконечно малом, неотличимом от прямой участке траектории) работу удобно выражать как скалярное произведение векторов силы и элементарного перемещения точки по траектории. В пространственной системе координат это можно записать как

Готовые работы на аналогичную тему

$\delta A = F_x \cdot dx + F_y \cdot dy + Fz \cdot dz$

, где $F_x, F_y, F_z$ — проекции силы на координатные оси, $dx, dy, dz$ — соответствующие изменения вектора траектории.

Угол между векторами силы и перемещения показывает ускоряющим или замедляющим является воздействие. Если угол острый — работа положительна, при тупом угле она, соответственно, отрицательна.

Представив расстояние как произведение скорости на время, можно найти соотношение между элементарной работой и импульсом:

$\delta A = \bar{F} \cdot \bar{v} \cdot dt = \bar{v} \cdot dp $

, где $v$ — скорость, $dt$ — промежуток времени, за который совершается работа, $dp$ — изменение импульса тела за этот промежуток.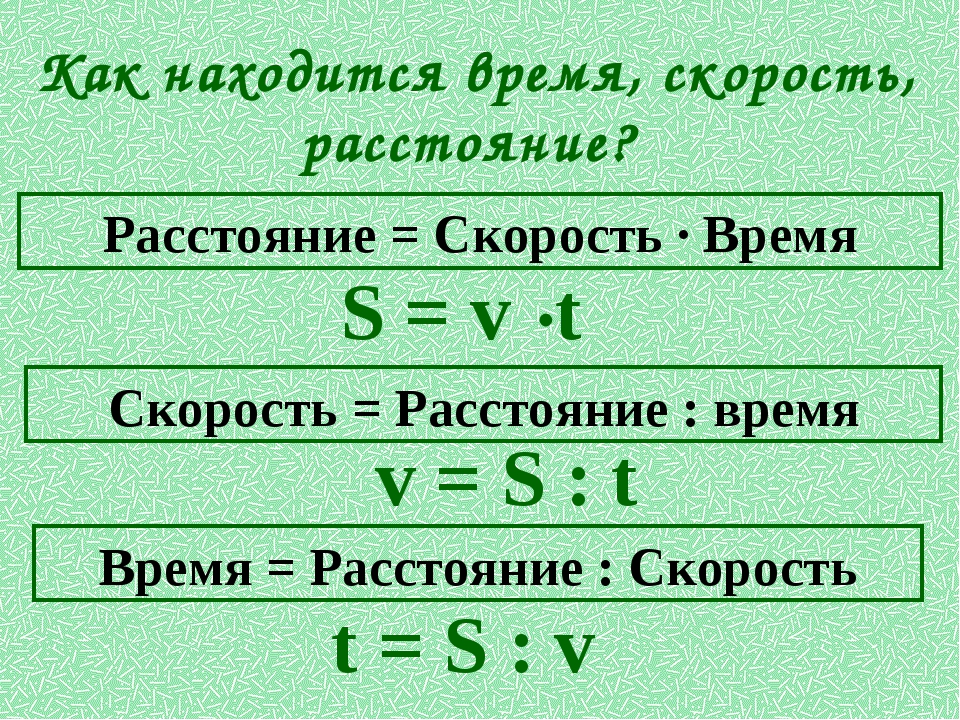

Если на физическое тело действуют сразу несколько сил, то следует провести векторное суммирование элементарных работ всех сил. При этом векторная сумма сил, действующих внутри тела, принимается равной нулю.

Работа для вращающегося тела определяется по формуле:

$\delta A = \bar{M} \cdot \bar{\omega} \cdot dt = \bar{M} \cdot d\bar{\phi}$

, где $\bar{M}$ — совокупный вращающий момент действующих на тело сил, $\bar{\omega}$ — мгновенная угловая скорость, $d\bar{\phi}$ — элементарный вектор поворота.

Кинематика – FIZI4KA

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.

При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( S \)​ — перемещение тела относительно неподвижной системы отсчета;
​\( S_1 \)​ — перемещение тела относительно подвижной системы отсчета;
​\( S_2 \)​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( v \)​ — скорость тела относительно неподвижной системы отсчета;
​\( v_1 \)​ — скорость тела относительно подвижной системы отсчета;

​\( v_2 \)​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Определим скорость второго тела относительно первого \( v_{21} \):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​\( \alpha \)​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.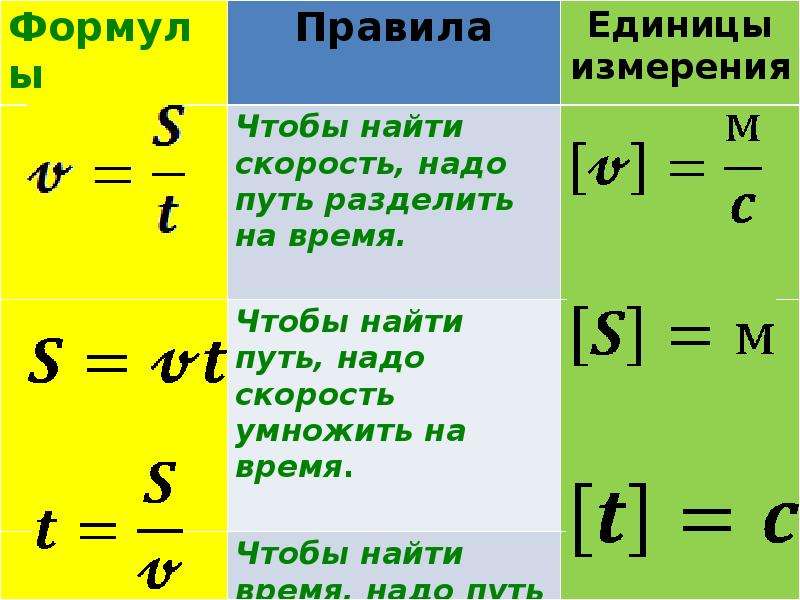

Обозначение — ​\( v \)​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.

Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​\( a \)​, единица измерения — м/с².
В векторном виде:

где ​\( v \)​ – конечная скорость; ​\( v_0 \)​ – начальная скорость;
​\( t \)​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​\( a_n \)​ – нормальное ускорение, ​\( a_{\tau} \)​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.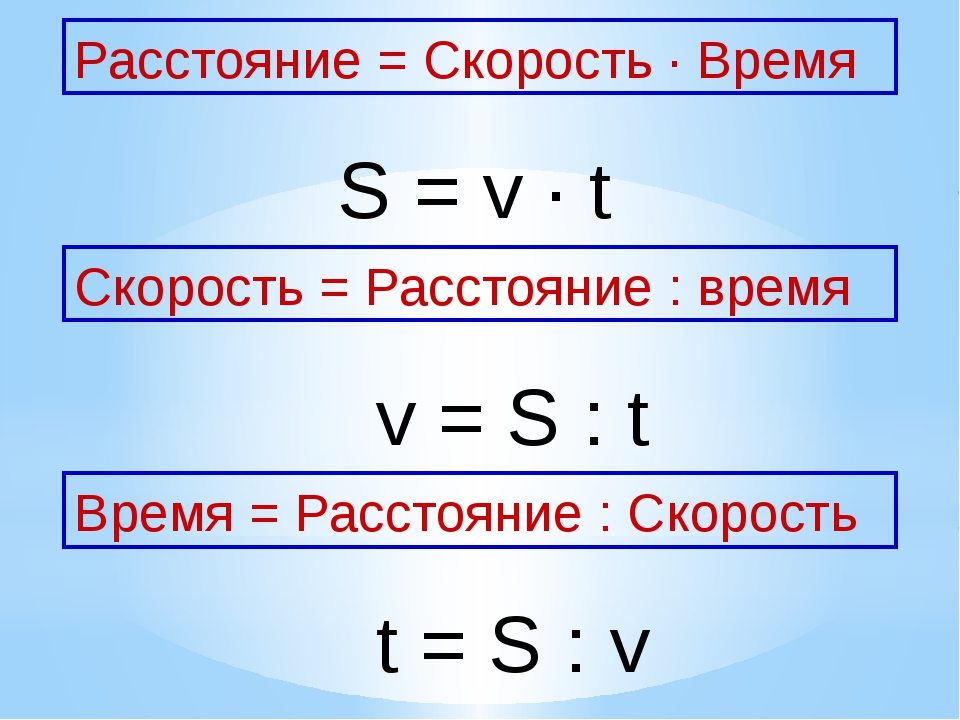
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, ​\( v \)​ ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.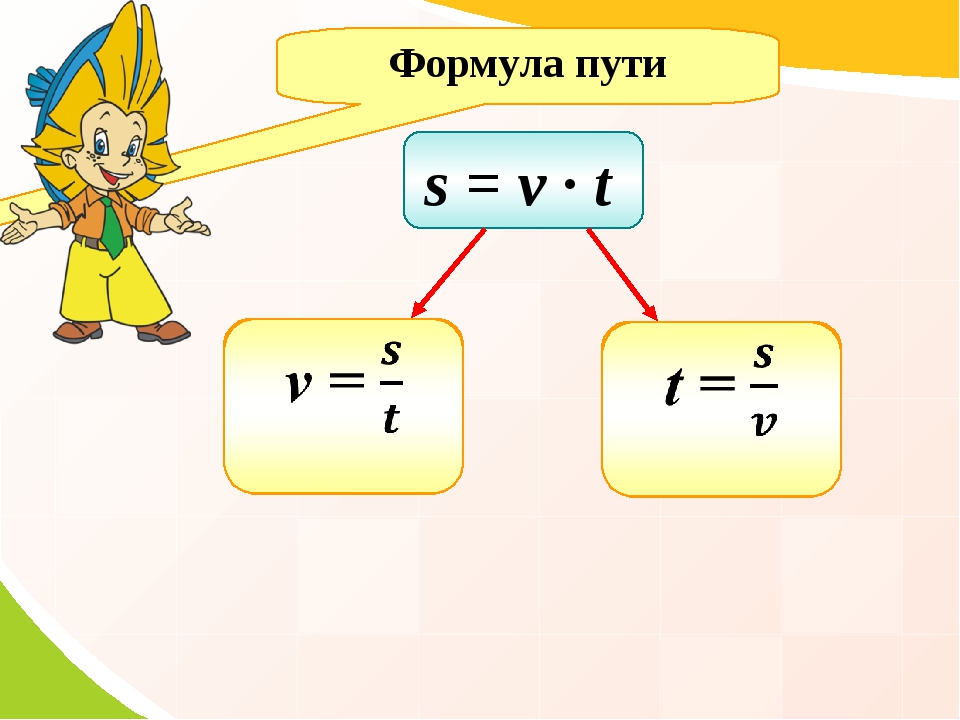
График 1 лежит над осью ​\( t \)​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​\( t \)​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​\( x=x(t) \)​.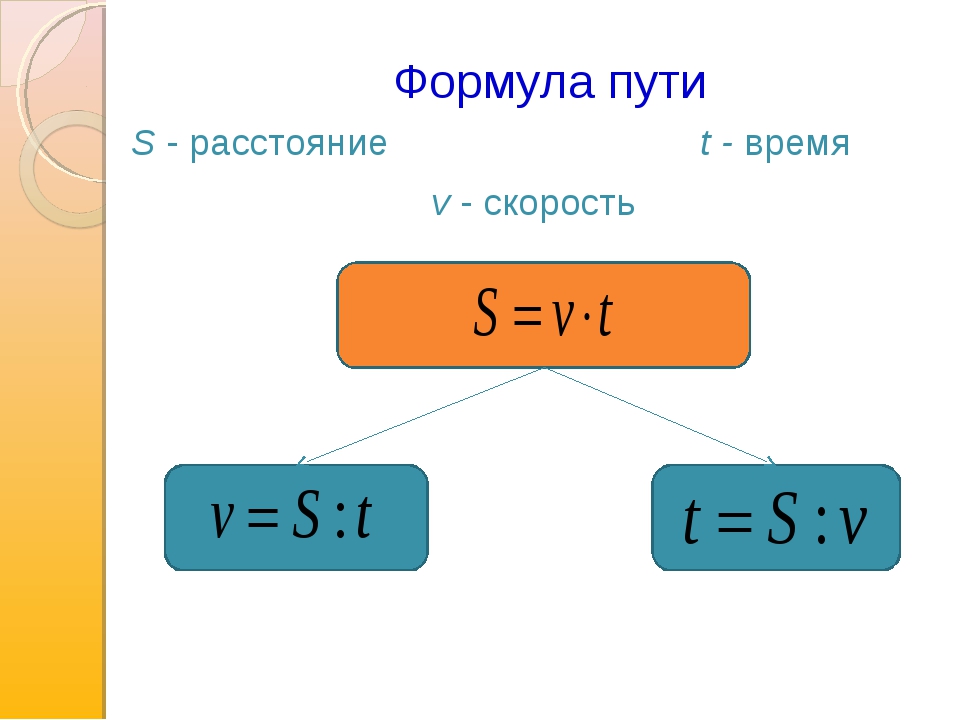

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​\( a_x \)​ > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​\( v_{0x} \)​ > 0, ​\( a_x \)​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_{0x} \) > 0, \( a_x \) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, \( v_{0x} \) < 0, \( a_x \) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​\( t_2-t_1 \)​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​\( n \)​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с².

Важно! \( g \) = 9,8 м/с², но при решении задач считается, что \( g \) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​\( a_{цс} \)​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​\( T \)​, единицы измерения – с.

где ​\( N \)​ – количество оборотов, ​\( t \)​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​\( \nu \)​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​\( v \)​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​\( \omega \)​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​\( v_1 \)​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​\( (m) \)​ равна нулю, мгновенная скорость в верхней точке ​\( (n) \)​ равна удвоенной скорости ​\( v_1 \)​, мгновенная скорость точки ​\( (p) \)​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​\( (c) \)​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

 

Кинематика

2.9 (58%) 10 votes

Перемещение и путь при равноускоренном прямолинейном движении 🐲 СПАДИЛО.РУ

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Задание EF18831 На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t₁=20 с до t₂=50 с.

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Исходные данные:

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s = s₁ + s₂

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

s₁+ s₂= 100 + 100 = 200 (м)

Ответ: 200

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

• перемещение и путь;
• скорость;
• ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Формула средней скорости движения

 

 

Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории

 

Средняя скорость движения —  это отношение полного пути пройденного объектом на общее время затраченное на это путешествие

 

 

Естественно предположить, что если объект часть общего пути прошел за одно время,  другую часть  за другое время, а третью за третье время, то  средняя скорость  будет являтся отношением  всех частей пути на все затраченное время.

 

 

А если  известно  например  части пути и скорость объекта на каждом пути ?  Не среднее арифметическое же брать от всех скоростей… хотя очень часто  именно так и поступают впервые большинство учеников, да и взрослых тоже

 

На самом деле, при известных частях пути и скоростей на участке формула будет следующая

 

 

наверняка догадались как она получилась из предыдущей формулы.

 

Если в задании пути буду обозначаться как часть от общего ( например,  первая половина пути, 2/3 пути и т.п.) то, учитывая  что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость  будет определятся как

 

Пример: 

Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.

Решение:

 

Ответ: 60 км/час

 

 

И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.

 

 

Правда есть еще четвертый вариант, но он практически никогда не встречается в задачах. Это когда встречаются комбинированные данные, например: Пешеход, преодолевает путь из точки А в точку Б. Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час. Какое расстояние  между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час

 

Смотрим вот на эту формулу    и думаем

 

Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)

Теперь со временем

На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути.  Не пугайтесь что получилось «время  равно одной десятой пути». Оно потом понадобится..

Время на втором участке известно и равно 1 час

 

Напишем нашу формулу по полученным данным

 

 

 

Выразим расстояние от точки А до точки Б через среднюю скорость и получим

 

 

Поставим значение средней скорости  получим что общее расстояние которое преодолел пешеход равно  4 километра и почти 286 метров

 

Сложновато? Зато интересно и увлекательно.

 

Из последней формулы  вытекает  «парадоксальный» вывод: При средней скорости приближающейся к 10 км/час  расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще  становится отрицательным.

 

Что хотелось бы по этому поводу сказать. не всегда надо бездумно подвергать анализу последнюю формулу, особенно когда знаменатель  обращается в ноль.

Взяв предыдущую формулу  — мы бы увидели что  при средней скорости в 10 км/ч , расстояние просто будет неопределено. То есть при заданных условиях средняя скорость никак не может быть больше 10 км/час.

 

 

• Фразеологический словарь выражения чувств и эмоций >>

Интерактивный калькулятор зависимости мощности от скорости на основе модели

Стив Гриббл · gribble [at] gmail [точка] com

Циклическая мощность и скорость

Изучите взаимосвязь между вашей велосипедной мощностью (мощностью) и скорость. Наведите курсор на график или нажмите на него, чтобы исследовать определенные точки. Измените поля ниже, и график обновится.

Наведите курсор на график, чтобы изучить распределение сил, задействованных на определенной скорости.

Определите удельную мощность или скорость

Физика, влияющая на езду на велосипеде с постоянной скоростью

На этой веб-странице используются физические модели сил велосипедиста, чтобы помочь вы оцениваете соотношение между мощностью P (ватт) и скорость V (км / ч или миль / ч) велосипедиста. Для этого вам понадобится оценить несколько параметров; приведены разумные значения по умолчанию.

Есть три основные силы, которые вы, как велосипедист, должны преодолеть, чтобы двигаться вперед:

• Гравитация: Если вы едете на велосипеде в гору, вы сражаетесь против силы тяжести, но если вы едете на велосипеде под гору, гравитация работает на вы.На этой странице измеряется крутизна холма с точки зрения процентная оценка G : подъем, деленный на пробег, умноженный на 100. Чем тяжелее вы и ваш велосипед, тем больше энергии вы должны тратить преодолеть гравитацию. Общий вес вас (велосипедиста) и ваш велосипед Вт (кг). Постоянная гравитационной силы г, равно 9,8067 (м / с ² ).

  
  Формула силы тяжести, действующей на велосипедиста, в метрических единицах. единиц, это:

  \ (\ qquad F _ {\ mbox {gravity}} = 9.8067 \ cdot \ sin (\ arctan (\ frac {G} {100})) \ cdot W \)
  

• Сопротивление качению: Трение между шинами и дорожное покрытие замедляет вас. Чем неровнее дорога, тем больше трение, которое вы испытаете; чем выше качество ваших шин и трубка, тем меньше трение вы испытаете. Кроме того, чем тяжелее вы и ваш велосипед, тем большее трение вы испытаете. Там безразмерный параметр, называемый коэффициентом прокатки . сопротивление , или C _rr , которое захватывает неровность дороги и качество ваших шин.

  
  Формула сопротивления качению, действующего на велосипедиста, в метрические единицы, это:

  \ (\ qquad F _ {\ mbox {Rolling}} = 9.8067 \ cdot \ cos (\ arctan (\ frac {G} {100})) \ cdot W \ cdot C_ {rr} \)
  

• Аэродинамическое сопротивление: При движении по воздуху ваше велосипед и тело должны толкать воздух вокруг вас, подобно тому, как снегоочиститель отталкивает снег. Из-за этого воздух оказывает против вас силу во время езды. Есть несколько вещей это диктует, сколько силы воздух оказывает против вас.В быстрее вы едете, скорость V (м / с), тем сильнее воздух толкает против вас. Кроме того, вы и ваш велосипед представляете определенную лобовая площадь А ( ^{м 2} ) в воздух. Чем больше это лобной области, тем больше воздуха вам нужно вытеснить и тем больше сила, которую воздух давит на вас. Вот почему велосипедисты и производители велосипедов изо всех сил стараются минимизировать площадь лобовой части в аэродинамическое положение. Плотность воздуха Rho (кг / м ³ ) тоже немаловажно; чем плотнее воздух, тем с большей силой это оказывает на вас.

  Наконец, есть и другие эффекты, такие как скользкость ваша одежда и степень ламинарного потока воздуха. чем бурно вокруг вас и вашего велосипеда. Оптимизация вашего в этом также помогают аэродинамические положения. Эти другие эффекты зафиксирован в другом безразмерном параметре, называемом перетаскиванием коэффициент , или C _d . Иногда вы увидите люди говорят о « C _d · A », или CdA .Это просто коэффициент лобового сопротивления C _d умножить на площадь лобной A . Если у вас нет доступа к аэродинамической трубе, трудно измерить C _d и A отдельно; вместо этого люди часто просто измерьте или сделайте вывод C _d · A как комбинированный номер.

  Формула аэродинамического сопротивления, действующего на велосипедиста, в метрические единицы, это:

  \ (\ qquad F _ {\ mbox {drag}} = 0.2 \)
  

Общая сила, противодействующая вам, велосипедисту, складывается из этих трех силы:

\ (\ qquad F _ {\ mbox {resist}} = F _ {\ mbox {gravity}} + F _ {\ mbox {Rolling}} + F _ {\ mbox {drag}} \)

На каждый метр, который вы циклически перемещаете вперед, вы тратите энергию на преодоление эта сила сопротивления. Общее количество энергии, которое вы должны потратить переместиться на расстояние D (м) против этой силы называется Работа (Джоули), которую вы выполняете:

\ (\ qquad \ mbox {Work} = F _ {\ mbox {resist}} \ cdot D \)

Если вы движетесь вперед со скоростью V (м / с), то вы должны поставлять энергию со скоростью, достаточной для работы по перемещению В метров каждую секунду.Этот уровень расхода энергии равен называется мощностью , и измеряется она в ваттах. Сила P _колесо (Вт), которое должно быть предоставлено вашему колеса велосипеда, чтобы преодолеть общую силу сопротивления F _{сопротивление} (Ньютонов) при движении вперед со скоростью В (м / с) составляет:

\ (\ qquad P _ {\ mbox {wheel}} = F _ {\ mbox {resist}} \ cdot V \)

Вы, велосипедист, являетесь двигателем, обеспечивающим эту мощность. {- 1} \ cdot \ left [\ left (9.2 \ right) \ right] \ cdot V \)

Одно из страшных последствий этого уравнения — то, что при высоком скорости, мощность, которую вы должны произвести, пропорциональна куб вашей скорости. Итак, чтобы увеличить скорость на 25%, вам нужно почти вдвое увеличить мощность!

Формула теста скорости набора, формула набора текста, формула слов в минуту

Индия Ввод

• Свяжитесь с нами
• Продайте свой сайт

Боковая панель

×

• Home
  • Набор текста на хинди
  • Набор текста на малаялам
  • Набор на гуджарати
  • Набор на маратхи
  • На тамильском языке
  • Набор на телугу
  • Набор на каннаде
  • Набор на пенджаби
  Набор на бенгали Набор текста на бенгальском Asamiya Typing
  • Sinhalese Typing
  • Urdu Typing
  • Arabic Typing
  • Nepali Typing
• Typing Tutor
  • Hindi Typing Tutor (Kruti Dev)
  • Advanced Hindi Typing Tutor / Reefing Hindy Typing (Manping Typing)
  • Inscript Hindi Typing Tutor
  • English Typing Tutor
  • Advanced English Typing Tutor
  • Hindi Type in Mobile
  • Voice to Text — Hindi
  • Voice to Text — English
• Typing Test
  • Hindi Typing Test
  • Крутидев / Девлис Тест на набор текста на хинди
  • Тест на набор текста в Unicode / Mangal на хинди
  • Тест на набор текста на хинди
  • Экзамен на набор текста — Krutidev, хинди
  • Экзамен на набор текста — Remington Gail
  • Экзамен на набор текста — Inscript на хинди
  • Тест на набор текста на английском языке
  • English Typing Test Advance
  • Typing Exam — English
  • Typing Certificate
  • Print Certificate
  • Verify Certificate
  • Typing Ranking
• Перевод
  • С английского на хинди
  • С хинди на английский
• Советы по вводу текста
  • Код символа Krutidev
  • Код Remington Gail
  • Код символа Inscript
  • Сочетания клавиш английского Alt-кода
  • Клавиатура Mangal / Remington
  • Клавиатура Inscript
  • Inscript Hindi Typing
  • Krutidev Hindi Typing
  • Hindi Me Type Kare
  • Помощь по набору текста с английского на хинди
  • Формула скорости набора
  • Научитесь быстро печатать
  • Инструкция теста набора текста
  • Языковая панель
  • Восстановить отсутствующую языковую панель

Скорость и скорость

Скорость и скорость

Скорость — это то, насколько быстро что-то движется.

Скорость — это скорость с направлением .

Говоря, что собака Ариэль бежит со скоростью 9 км / ч, (километров в час) — это скорость.

Но сказать, что он бежит 9 км / ч на запад — это скорость.

	Скорость	Скорость
Имеет:	звездная величина	звездная величина и направление
Пример:	60 км / ч	60 км / ч Север
Пример:	5 м / с	5 м / с вверх

Представьте, что что-то движется вперед и назад очень быстро: у него высокая скорость, но низкая (или нулевая) скорость.

Скорость

Скорость измеряется как расстояние, пройденное с течением времени.

Скорость = Расстояние Время

Пример: автомобиль проезжает 50 км за час.

Его средняя скорость составляет 50 км в час (50 км / ч)

Скорость = Расстояние Время знак равно 50 км 1 час

Мы также можем использовать эти символы:

Скорость = Δs Δt

Где Δ (« Delta ») означает «изменение», а

• с означает расстояние («с» для «пробела»)
• т означает время

Пример: вы пробегаете 360 м за 60 секунд.

Скорость = Δs Δt

= 360 м 60 секунд

= 6 месяцев 1 секунда

Значит, ваша скорость 6 метров в секунду (6 м / с).

шт.

Скорость обычно измеряется в:

• метра в секунду (м / с или мс ^-1 ), или
• километров в час (км / ч или км ч ^-1 )

км — это 1000 м, а в часе 3600 секунд, поэтому мы можем выполнить преобразование следующим образом (см. Метод преобразования единиц, чтобы узнать больше):

1 метр 1 с × 1 км 1000 м × 3600 с 1 ч знак равно 3600 м · км · с 1000 с · м · ч знак равно 3.6 км 1 ч

Так 1 м / с равно 3,6 км / ч

Пример: Что такое 20 м / с в км / ч?

20 м / с × 3,6 км / ч 1 м / с = 72 км / ч

Пример: Что такое 120 км / ч в м / с?

120 км / ч × 1 м / с 3,6 км / ч = 33,333 … м / с

Средняя и мгновенная скорость

В примерах до сих пор вычисляется средняя скорость : как далеко что-то перемещается за период времени.

Но скорость может измениться со временем. Автомобиль может ехать быстрее и медленнее, может даже останавливаться на светофоре.

Итак, существует также мгновенная скорость : скорость в мгновение во времени. Мы можем попытаться измерить его, используя очень короткий промежуток времени (чем короче, тем лучше).

Пример: Сэм использует секундомер и измеряет 1,6 секунды, когда машина проезжает между двумя столбами на расстоянии 20 м друг от друга. Что такое мгновенная скорость ?

Что ж, мы не знаем точно, так как машина могла ускоряться или замедляться в течение этого времени, но мы можем оценить:

20 метров 1.6 с = 12,5 м / с = 45 км / ч

Это действительно все еще средняя, ​​но близкая к мгновенной скорости.

Постоянная скорость

Когда скорость не меняется, это постоянная .

Для постоянной скорости средняя и мгновенная скорости одинаковы.

Скорость

Скорость — это скорость с направлением .

Это на самом деле вектор …

… поскольку он имеет звездную величину и направление

Поскольку направление важно, скорость использует смещение вместо расстояния:

Скорость = Расстояние Время

Скорость = Рабочий объем Время в направлении.

Пример: вы идете от дома до магазина за 100 секунд, какова ваша скорость и какова ваша скорость?

Скорость = 220 метров 100 с = 2,2 м / с

Скорость = 130 кв.м 100 с Восток = 1,3 м / с Восток

Вы забыли свои деньги, поэтому поворачиваетесь и возвращаетесь домой еще через 120 секунд: какова ваша скорость и скорость туда и обратно?

Общее время 100 с + 120 с = 220 с:

Скорость = 440 м 220 с = 2.0 м / с

Скорость = 0 м 220 с = 0 м / с

Да, скорость равна нулю, когда вы закончили там, где начали.

Узнайте больше на Vectors.

Родственник

Движение относительно. Когда мы говорим, что что-то «покоится» или «движется со скоростью 4 м / с», мы забываем сказать «по отношению ко мне» или «по отношению к земле» и т. Д.

Подумайте вот о чем: вы действительно стоите на месте? Вы находитесь на планете Земля, которая вращается со скоростью 40 075 км в день (около 1675 км / ч или 465 м / с) и движется вокруг Солнца со скоростью около 100 000 км / ч, которое само движется через Галактику.

В следующий раз, когда вы будете гулять, представьте, что вы неподвижны, и это мир движется у вас под ногами. Чувствует себя прекрасно.

Это все относительно!

Скорость звука Формулы

Возмущение, внесенное в какую-либо точку вещества — твердого или жидкого, — будет распространяться через вещество как волна с конечной скоростью.

Акустическая скорость и скорость звука

Скорость, с которой небольшое возмущение будет распространяться через среду, называется Акустическая скорость или Скорость звука.

Скорость звука связана с изменением давления и плотности вещества и может быть выражена как

c = (dp / dρ) ^1/2 (1)

где

c = скорость звука (м / с, фут / с)

dp = изменение давления (Па, фунт / кв. Дюйм)

dρ = изменение плотности (кг / м ³ , фунт / фут ³ )

Скорость звука в газах, жидкостях и твердых телах

Акустическая скорость также может быть выражена с помощью закона Хука как

c = (K / ρ) ^1/2 (2)

, где

K = объемный модуль упругости (Па, фунт / кв. Дюйм)

ρ = плотность (кг / м ³ , фунт / фут ³ )

Это уравнение действительно для жидкостей , твердые вещества и газ es.Звук быстрее распространяется через среды с более высокой эластичностью и / или меньшей плотностью. Если среда вообще несжимаема — несжимаема — скорость звука бесконечна ( c ≈ ∞).

• свойства при 1 бар и 0 ^o C

Скорость звука — скорость звука — в идеальных газах

Поскольку акустические возмущения, вносимые в точку, очень малы, теплопереносом можно пренебречь и для газов предполагается изэнтропический. Для изоэнтропического процесса можно использовать закон идеального газа, а скорость звука можно выразить как

c = (kp / ρ) ^1/2

= (k RT) ^1/2 (3)

, где

k = отношение удельных теплоемкостей (адиабатический индекс)

p = давление (Па, фунт / кв. Дюйм)

R = индивидуальная газовая постоянная (Дж / кг · K, фут-фунт / оторочка ^o R)

T = абсолютная температура ( ^o K, ^o R)

Для идеального газа скорость звука пропорциональна корень квадратный из абсолютной температуры.

Пример — Скорость звука в воздухе

Скорость звука в воздухе при 0 ^o C (273,15 K) и абсолютном давлении 1 бар можно рассчитать как

c = (1,4 (286,9 Дж / K кг) (273,15 K)) ^1/2

= 331,2 (м / с)

где

k = 1,4

и

R = 286.9 (Дж / К кг)

Скорость звука в воздухе при 20 ^o C (293,15 K) и абсолютном давлении 1 бар можно рассчитать как

c = (1,4 (286,9 Дж / K кг) (293,15 K)) ^1/2

= 343,1 (м / с)

Пример — Скорость звука в воде

Скорость звука в воде при 0 ^o C можно рассчитать как

c = ((2.